Orde en chaos in het klimaat

Ooit, lang geleden, kon je op zondag, ik meen na de voetbalsamenvattingen van Studio Sport, naar de Lotto-trekking kijken. Die verliep via een vaste procedure. Eenenveertig genummerde balletjes zaten keurig op volgorde in een houder waaruit ze allemaal tegelijk werden losgelaten. Ze vielen in een grote, bol van plexiglas die even ronddraaide. Na een aantal rotaties keerde de draairichting om, waardoor enkele balletjes in een gootje terechtkwamen. Het eerste balletje in het gootje kwam naar buiten. Het hele procedé herhaalde zich nog zes keer, en daarmee had je de uitslag van zes winnende getallen plus een reservegetal.

Wat mij fascineerde, was dat dat helemaal identieke proces elke keer een andere uitkomst opleverde. Blijkbaar was ik als kind al geneigd tot deterministisch denken. En dat bracht me bij de voor de hand liggende verklaring. Natuurlijk zijn die balletjes niet helemaal perfect rond, is het materiaal waar ze van gemaakt zijn niet overal exact even dik of zwaar, of kunnen kleine verschillen in temperatuur of luchtdruk ervoor zorgen dat de balletjes net iets anders over elkaar rollen. Zo konden hele kleine, op het oog onwaarneembare verschillen de trekking perfect onvoorspelbaar maken. Het is, leerde ik pas veel later, een voorbeeld van gevoelige afhankelijkheid (sensitive dependence). En dat begrip is waar het in de chaostheorie om draait: deterministische processen die toch een onvoorspelbaar verloop hebben.

De paradox van deterministische chaos

Er zit een paradox in een chaotisch systeem, zoals de lottoballetjesmachine. Alles wat er gebeurt, verloopt volgens vrij eenvoudige natuurwetten van oorzaak en gevolg. En toch is de uitkomst in onze beleving puur toeval. Maar omdat die wetten van oorzaak en gevolg van toepassing zijn, zit er altijd wel een grens aan dat toeval. Er kwam nooit meer dan één balletje tegelijk uit de machine. Het getal op dat balletje was nooit groter dan 41. En dat er in plaats van een lottoballetje ineens een kaasblokje naar buiten kwam was uitgesloten. Voor een lottoballetjesmachine heb je natuurlijk geen complexe theorie nodig om dergelijke grenzen van het toeval in te zien. Voor andere chaotische (of, in jargon: non-lineaire dynamische) systemen liggen die grenzen nog wel eens minder voor de hand. En daar kan de kennis van de chaostheorie behulpzaam zijn.

Chaos wordt vaak geassocieerd met complexiteit, maar de lottoballetjesmachine laat zien dat een vrij eenvoudig systeem ook chaotisch gedrag kan vertonen. Edward Lorenz, de Amerikaanse meteoroloog die wordt gezien als een van de grondleggers van de chaostheorie, kreeg het na een tijd zoeken zelfs voor elkaar om chaotisch gedrag in een computer te simuleren met maar drie eenvoudige wiskundige vergelijkingen. Het waren sterke vereenvoudigingen van de roemruchte Navier-Stokesvergelijkingen uit de stromingsleer, die onder meer de bewegingen beschrijven van lucht in de atmosfeer, en van water in rivieren en oceanen. Door die vereenvoudigingen kwamen de simulaties nauwelijks nog overeen met wat er in de fysische werkelijkheid gebeurt, maar daar ging het Lorenz dan ook niet om. Hij liet zien dat chaotisch gedrag onderzocht kan worden als puur wiskundig probleem. Het duurde even tot andere wiskundigen het oppikten, maar toen dat uiteindelijk gebeurde leverde dat theoretische kennis op die in tal van wetenschappelijke disciplines toepasbaar bleek: van meteorologie tot economie tot medische wetenschap.

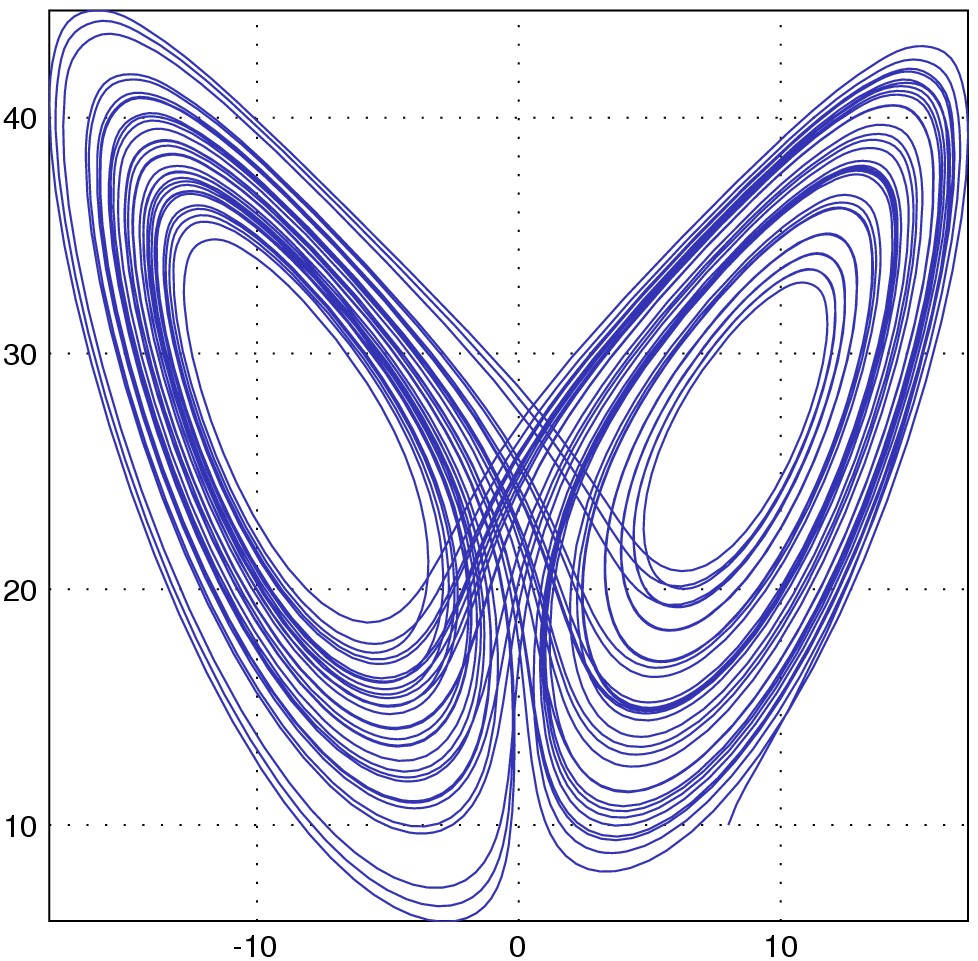
Het bekende vlindervormige plaatje dat een icoon is geworden van de chaostheorie volgt uit de drie vergelijkingen van Lorenz. Het laat zien hoe de toestand van een systeem dat door die vergelijkingen wordt beschreven zich in de tijd ontwikkelt. In jargon heet die vlinder de Lorenz-attractor. Eigenlijk zou die attractor of aantrekker in drie dimensies weergegeven moeten worden. Het systeem wordt als het ware aangetrokken door toestanden die zich op de vleugels van de vlinder bevinden en soms springt het van de ene naar de andere vleugel. Maar in de sprongen zit geen enkele regelmaat, hoelang de simulatie ook blijft draaien. Wordt de simulatie gestart vanuit een toestand die buiten de aantrekker ligt, dan zal het gedrag zich in de richting van de aantrekker bewegen. De aantrekker is dus een evenwichtstoestand van een systeem dat permanent en onvoorspelbaar verandert. Alweer een paradox. Het is niet voor niets dat zo’n evenwichtstoestand in een chaotisch systeem een ‘strange attractor’ wordt genoemd. (Er is nog wel meer vreemd aan die aantrekker, maar het gaat te ver om daar in detail op in te gaan.)

Begrensde oneindigheid

Het vreemde en paradoxale komt nog meer naar voren in de wiskunde. Zo begrenst de strange attractor de mogelijke toestanden waarin een chaotisch systeem zich kan bevinden, maar is het aantal mogelijke toestanden binnen die begrenzing nog steeds oneindig groot. De wiskundige beschrijving van de attractor is dan een oneindig lange curve, binnen een eindige ruimte van drie of meer dimensies, die zichzelf nergens snijdt of raakt. Als dat wel zou gebeuren zou dat immers betekenen dat immers een herhaling van dezelfde toestand betekenen. En omdat alle processen in het systeem deterministisch zijn, zou dat tot een cyclisch verloop moeten leiden. De gevoelige afhankelijkheid van zo’n systeem impliceert wel dat dat alleen gebeurt als die toestanden tot eindeloos veel cijfers achter de komma identiek zijn.

Complexe fysische systemen hebben ook zulke aantrekkers, maar er zijn vaak (veel) meer dan drie dimensies nodig om die grafisch weer te geven. De crux is dat zo’n systeem onvoorspelbaar is, maar dat de onvoorspelbaarheid wel binnen de grenzen van de aantrekker blijft. Wordt het systeem van buitenaf beïnvloed, dan kan de vorm van de aantrekker veranderen en kunnen er dus toestanden ontstaan die eerder onmogelijk waren.

Niet alle inzichten van deze theorie kwamen als een totale verrassing. Natuurlijk niet: omdat de chaos ontstaat uit deterministische processen is vaak wel te beredeneren waarom een systeem onvoorspelbaar is. Fourier deed dat bijvoorbeeld al in de vroege negentiende eeuw. Aan de hand van natuurwetten kun je veel geïsoleerde processen prima voorspellen, maar buiten het wetenschappelijke laboratorium bestaan er geen geïsoleerde processen. Hij zag in dat de interacties van al die processen, die op zich goed werden begrepen, veel moeilijker voorspelbaar zijn. De Franse wiskundige Henri Poincaré constateerde in een beschouwing van het drielichamenprobleem (tegenwoordig bekend van Netflix) dat ook vrij eenvoudige deterministische systemen soms niet eenvoudig voorspeld kunnen worden, ook al zijn de natuurwetten die het gedrag van zo’n systeem bepalen bekend. Met een beetje goede wil zou je kunnen zeggen dat meteorologen ook al zoiets als een aantrekker hadden ontdekt: het klimaat. Je kon het weer weliswaar niet voorspellen, maar het gemiddelde over 30 jaar gaf toch een behoorlijk idee van wat je zou kunnen verwachten.

Het nieuwe van de chaostheorie was dat de onvoorspelbaarheid niet meer wordt gezien als een gegeven dat je maar moet accepteren, maar als iets met zijn eigen karakteristieken, patronen en wetten die in wiskunde te vangen zijn. Blijkbaar was het een onderwerp dat rond 1970 in de lucht hing, want naast Lorenz waren er verschillende anderen die zich er, grotendeels onafhankelijk van elkaar, in verdiepten. Helemaal toevallig was dat niet. De komst van de computer maakte het mogelijk om sets van vergelijkingen die chaotisch gedrag vertoonden uitgebreid door te rekenen en zo het gedrag ervan te verkennen. Het was experimentele wiskunde, op een manier die de wereld niet eerder had gezien. Wiskunde die aardig wat nieuwe inzichten opleverde, maar die niet altijd even eenvoudig naar de fysieke realiteit te vertalen was. En is, zoals verderop in dit verhaal zal blijken. Veel fysische chaotische systemen zijn namelijk een stuk complexer dan het drielichamenprobleem of de dubbele slinger. Zomaar even de vreemde aantrekker(s) bepalen van bijvoorbeeld een compleet ecosysteem is niet mogelijk.

Onvoorstelbaar onvoorspelbaar

Maar hoe ingewikkeld ook, de theorie leverde wel belangrijke nieuwe inzichten op. Dat begon al bij Lorenz. Het weer maanden vooruit voorspellen, zoals destijds de ambitie was van veel meteorologen, was onmogelijk en zou onmogelijk blijven, constateerde die. Aan de uitleg kwam weer een vlinder te pas: de vlinder in Brazilië die met een vleugelslag een tornado veroorzaakt in Texas. Het was een metafoor voor gevoelige afhankelijkheid. Want dat dat echt zou kunnen, vond Lorenz niet heel aannemelijk. Het is maar moeilijk voorstelbaar hoe zoiets zou kunnen gebeuren. Dat is relevant, want we hebben het immers over deterministische chaos: alles in de chaos verloopt via fysische mechanismes die de natuurwetten volgen. En het valt niet mee om een mechanisme te bedenken voor een vlinder die een tornado veroorzaakt. De vlindervleugel kan in elk geval in de verste verte niet de energie leveren voor een tornado. Die energie komt van de zon. Je zou je misschien wel voor kunnen stellen dat een flapperende vlindervleugel een wervel in de lucht een fractie versterkt, waardoor die net een kritische grens bereikt waardoor een op die plek een thermiekbel ontstaat. Die anders misschien een stukje verderop was ontstaan. Daardoor zou dan een grotere wervel weer net iets af kunnen buigen. Wat uiteindelijk dan zou kunnen leiden tot een andere koers van een compleet weersysteem. Wie weet is zoiets ooit in de lange geschiedenis van de aarde wel eens een keer gebeurd.

En daarmee komen we bij de aanleiding voor dit stuk: een onlangs verschenen artikel dat bewijs vindt voor iets dat wel wat lijkt op het vlindereffect. Volgens dit onderzoek zouden bewegingen van individuele moleculen uiteindelijk invloed hebben op de wervelingen op alle schaalniveaus die optreden in turbulent stromende gassen en vloeistoffen. Aan die conclusie wil ik niks afdoen, als is het maar omdat het een knap ingewikkeld artikel is, dat niet zomaar even te doorgronden is. Maar aan het eind trekken de auteurs een conclusie, die in een Youtube-filmpje werd overgenomen door Sabine Hossenfelder, die laat zien dat ze moeite hebben om de chaostheorie te vertalen naar de praktijk. Die van meteorologen en klimaatwetenschappers, om precies te zijn. Het komt erop neer dat ze zeggen dat weer- en klimaatmodellen de atmosfeer nooit perfect zullen kunnen simuleren, hoe fijnmazig de resolutie ervan ook is. Dat is niet onwaar, maar het is ook niets nieuws. Lorenz trok diezelfde conclusie meer dan zestig jaar geleden al. Maar zijn argumentatie was een stuk beter.

Chaos in de wetenschappelijke praktijk

Lorenz wees erop dat de belangrijkste beperking zit in de waarnemingen die de basis vormen van een weersvoorspelling, en dus ook van de simulaties van weermodellen. Er zijn geen waarnemingen van alle individuele vlinders, of van de thermische bewegingen van alle individuele luchtmoleculen. Bekijk je het puur vanuit de chaostheorie, dan zou het zinloos zijn om de resolutie van modellen fijnmaziger te maken dan die van waarnemingen via weerstations en -satellieten. Maar vanuit de onderliggende deterministische fysica zou het wel degelijk zinnig kunnen zijn, om processen die zich op kleinere schaal afspelen beter te simuleren. Het model zou dan nog steeds niet het effect van een individuele vlinder voorspellen, maar misschien wel iets beter de specifieke ontwikkeling van wolken simuleren. Dat geldt niet alleen voor weer-, maar ook voor klimaatmodellen. Die overigens al helemaal niet bedoeld zijn om de variaties in het systeem te voorspellen. De klimaatwetenschap kijkt onder meer naar de factoren die de strange attractor zouden kunnen veranderen, en we kunnen redelijkerwijs uitsluiten dat ze daarbij rekening moeten houden met fladderende vlindervleugeltjes of de thermische bewegingen van individuele moleculen.

Een ander punt van belang noemen de auteurs van het nieuwe artikel zelf. Hun resultaten gelden ‘in the absence of any larger disturbances’. Dergelijke grotere verstoringen zijn in het klimaatsysteem alomtegenwoordig: bergketens die luchtstromingen laten stijgen en dalen, temperatuurverschillen tussen land en zee, ijskappen en zee-ijs, de rotatie van de aarde, de schuine stand van de aardas, enzovoort. De invloed van al die factoren op circulatiepatronen in de atmosfeer is zo goed als oneindig veel groter dan de luchtverplaatsing door een toevallig passerend vlindertje.

Meteorologen die halverwege de twintigste eeuw meewerkten aan de bouw van de allereerste weermodellen hebben wel eens gezegd dat, achteraf, de minuscule rekenkracht van hun computers een zegen was. Ze hadden geen andere keus dan heel selectief die onderdelen uit het systeem te pikken die met een grove resolutie toch vrij goed gesimuleerd konden worden. Ze verloren zich niet in teveel details, omdat hun computers dat onmogelijk maakten. Dankzij grondige kennis van de fysica van het systeem lukte het vrij goed om hoofd- en bijzaken te onderscheiden, en daarna was het een kwestie van leren van wat er wel en niet goed ging in de simulaties. Een werkwijze die langzaamaan betere modellen opleverde en tegelijkertijd meer inzicht in de werking van de atmosfeer. Inclusief het chaotische gedrag, toen Lorenz dat eenmaal op het spoor was gekomen.

Kleine verschillen worden groot

De complexe wiskunde die theoretici van de chaos in de loop van de tijd hebben ontwikkeld, valt niet zomaar in te passen in weer- en klimaatmodellen. Maar er is wel een manier om de chaos mee te nemen in simulaties, en die is verrassend eenvoudig. In feite doen meteorologen nu opzettelijk wat Lorenz per ongeluk deed, en waarmee hij het fenomeen chaos op het spoor kwam. Lorenz wilde een simulatie die hij had uitgevoerd met een eenvoudig, door hemzelf gebouwd weermodel nog een keer herhalen, maar hij besloot het eerste stuk ervan over te slaan. Hij voerde tussenresultaten van de vorige simulatie in, startte het model en ging even koffie drinken. Toen hij terugkwam zag hij tot zijn verbazing dat de nieuwe simulatie een totaal andere weersituatie liet zien. Toen hij de twee simulaties meer in detail met elkaar vergeleek, zag hij dat de tweede langzaamaan divergeerde van de eerste. En toen begreep hij wat er aan de hand was. Hij had zijn tussenresultaten tot drie cijfers achter de komma ingevoerd, maar het model rekende met zes decimalen. Dat minuscule verschil zorgde ervoor dat de tweede simulatie eerst een heel klein beetje afweek van de eerste, maar geleidelijk aan steeds meer. En na verloop van tijd was er helemaal geen overeenkomst meer.

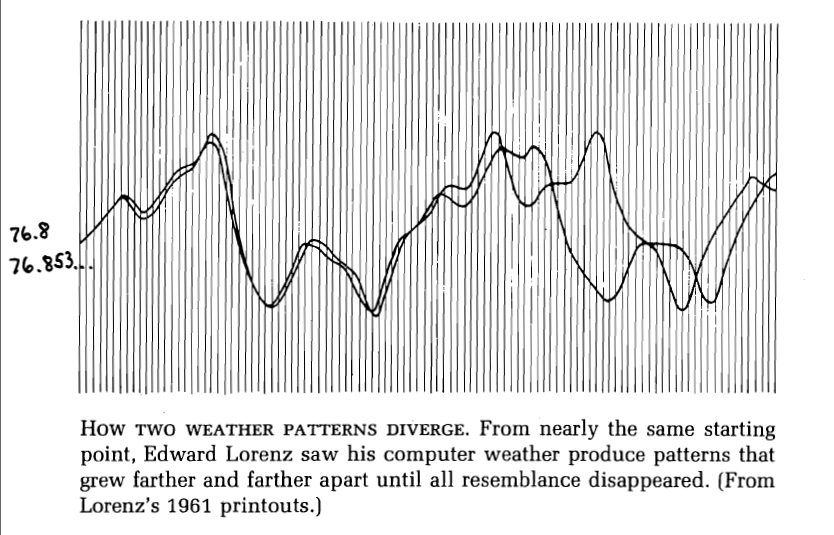
De les: om rekening te houden met de chaos in het systeem moet je meerdere simulaties uitvoeren, met kleine verschillen in de initiële condities. En dat is wat meteorologen en klimaatwetenschappers dan ook doen. Door dat een beetje slim aan te pakken, bijvoorbeeld door een variatie in de initialisatie aan te brengen die overeenkomt met de onzekerheid in metingen, ontstaat er dan een beeld van wat er kan gebeuren. Bijvoorbeeld over het te verwachten weer tot twee weken vooruit. Soms is het beeld daarover behoorlijk duidelijk, en soms gaan de simulaties alle kanten op en is er dus niet zoveel over te zeggen. Verwachtingen voor de ontwikkeling van El Niño’s en La Niña’s zijn ook gebaseerd op meerdere modelruns. (En vaak ook op meerdere modellen.)

Ook op andere manieren wordt de kennis over chaos toegepast in het klimaatonderzoek. Nobelprijswinnaar Klaus Hasselmann deed dat bijvoorbeeld in de jaren ’70, door met een vrij eenvoudig model de interactie tussen snel en traag reagerende systemen te onderzoeken. Het leverde belangrijke kennis op over hoe de wisselwerking tussen de oceaan en de atmosfeer zorgt voor interne variabiliteit in het klimaat. Daarop voortbordurend legde hij een basis voor de methodes die worden gebruikt in detectie- en attributieonderzoek. Waar Lorenz door een fysisch model bij toeval op het spoor werd gezet van chaos als wiskundig probleem, koos Hasselmann bewust voor de invalshoek van de wiskunde. Om van daaruit het fysische systeem beter te begrijpen.

In zijn beroemde boek over chaos beschreef James Gleick nog maar eens een mooie paradox die volgt uit de chaostheorie: eenvoudige systemen kunnen zich soms opmerkelijk complex gedragen, terwijl het gedrag van complexe systemen soms opmerkelijk eenvoudig blijkt te zijn. Dat laatste is wel relatief, omdat die eenvoud niet altijd makkelijk te vinden is. Of uit te leggen. Aan dat laatste waag ik me hier maar niet. Want dit stuk is al lang genoeg.